Oblasť kruhu: vzorec. Prečo je plocha kruhu opísaná a vpísaná do štvorca rovná pravouhlému rovnoramennému trojuholníku, pravouhlému rovnoramennému lichobežníku?

Ako nájsť oblasť kruhu? Najprv nájdite polomer. Naučte sa riešiť jednoduché a zložité úlohy.

Kruh je uzavretá krivka. Akýkoľvek bod na kruhovej čiare bude rovnako vzdialený od stredu. Kruh je plochý tvar, takže riešenie úlohy nájsť oblasť je jednoduché. V tomto článku zvážime, ako nájsť oblasť kruhu vpísanú do trojuholníka, lichobežníka, štvorca a opísanú v blízkosti týchto obrázkov.

Oblasť kruhu: vzorec s použitím polomeru, priemeru, dĺžky kruhu, príklady riešenia úloh

Na nájdenie oblasti ​​číslo, musíte vedieť, že taký je polomer, priemer a číslo π.

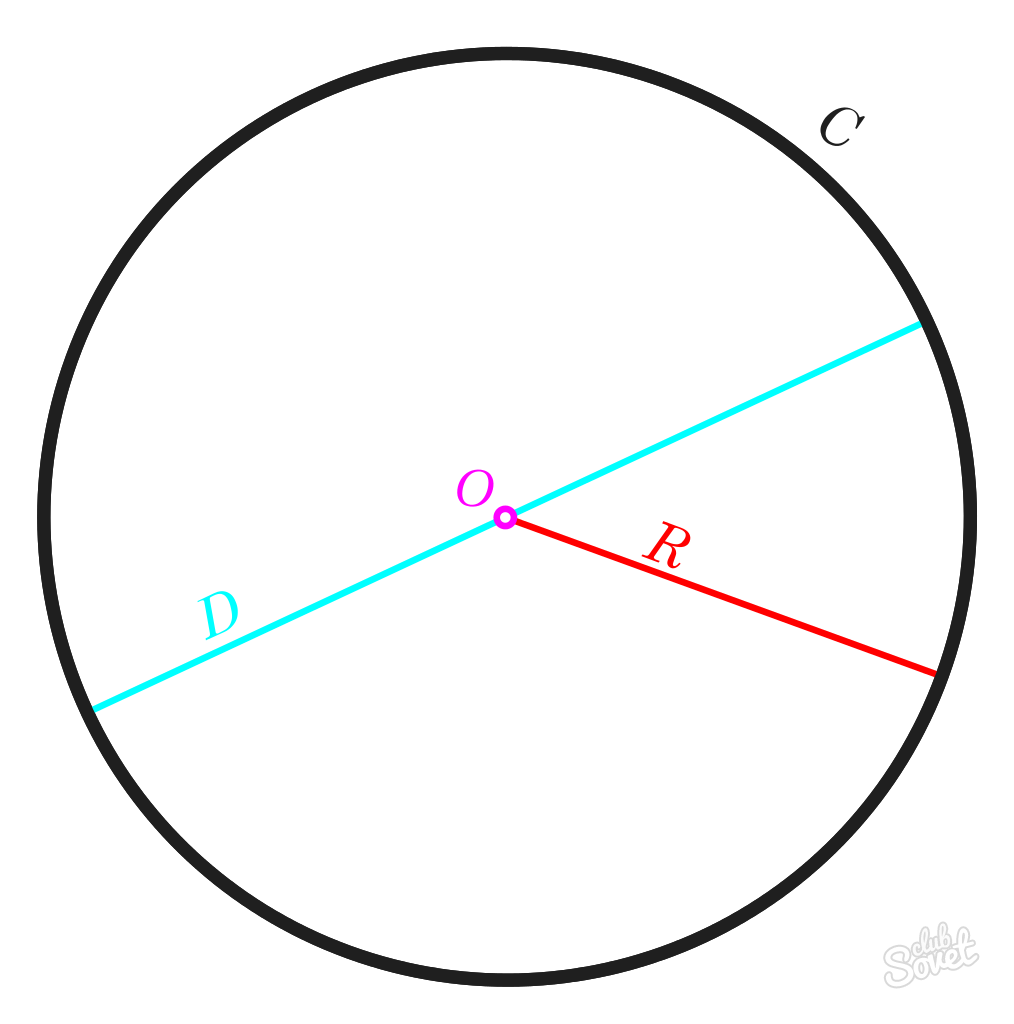
Polomer R je vzdialenosť ohraničená stredom kružnice. Dĺžky všetkých R-polomerov jedného kruhu budú rovnaké.

Priemer D je priamka medzi ľubovoľnými dvoma bodmi kružnice prechádzajúcej stredom. Dĺžka tohto segmentu sa rovná dĺžke polomeru R vynásobenej 2.

Číslo π je konštantná hodnota rovnajúca sa 3,1415926. V matematike sa toto číslo zvyčajne zaokrúhľuje na 3,14.

Vzorec na nájdenie plochy kruhu cez polomer:

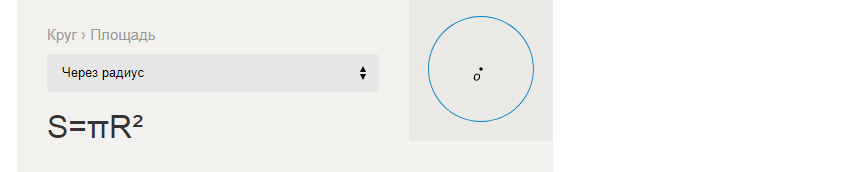
Príklady riešenia úloh na nájdenie S-plochy kruhu cez R-polomer:

---------- ----------------------------- --

Úloha: Nájdite obsah kruhu, ak je jeho polomer 7 cm.

Riešenie: S=πR2, S=3,14*72, S=3,14*49=153,86 cm2.

Odpoveď: Plocha kruhu je 153,86 cm2.

Vzorec na nájdenie S-plochy kruhu cez D-priemer:

Príklady riešenia úloh na nájdenie S, ak je známe D:

--------- --------------------------------

Úloha: Nájdite S kruhu, ak sa jeho D rovná 10 cm.

Riešenie: P=π*d2/4, P=3,14*102/4=3,14*100/4=314/4=78,5 cm2.

Odpoveď: Plocha plochej okrúhlej postavy je 78,5 cm2.

Nájdenie S kruhu, ak je známa dĺžka kruhu:

Najprv zistíme, aký je polomer. Dĺžka kruhu sa vypočíta podľa vzorca: L=2πR, podľa toho sa polomer R bude rovnať L/2π. Teraz nájdeme oblasť kruhu pomocou vzorca cez R.

Uvažujme riešenie na príklade úlohy:

----------- -----------------------------

Úloha: Nájdite obsah kruhu, ak je známa dĺžka kruhu L — 12 cm.

Riešenie: Najprv zistíme polomer: R=L/2π=12/2*3,14=12/6,28=1,91.

Teraz nájdeme plochu cez polomer: S=πR2=3,14*1,912=3,14*3,65=11,46 cm2.

Odpoveď: Plocha kruhu je 11,46 cm2.

Oblasť kruhu vpísaného do štvorca: vzorec, príklady riešenia úloh

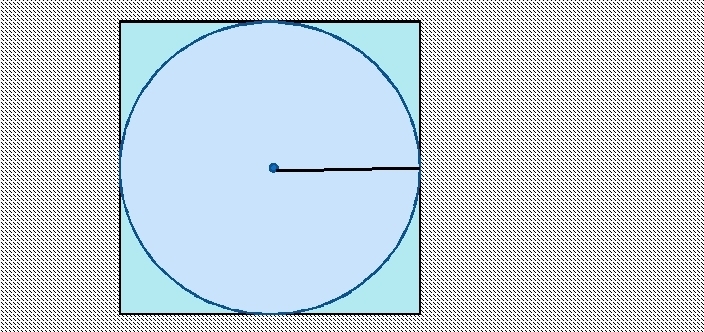
Nájdenie obsahu kruhu vpísaného do štvorca je jednoduché. Strana štvorca je priemer kruhu. Ak chcete nájsť polomer, musíte stranu vydeliť 2.

Vzorec na nájdenie plochy kruhu vpísaného do štvorca:

Príklady riešenia úloh na nájdenie plochy kružnice vpísanej v štvorec:

---------------------------------- ----

Úloha č.1: Známa je strana štvorcového obrazca, ktorá sa rovná 6 centimetrom. Nájdite S-oblasť vpísaného kruhu.

Riešenie: S=π(a/2)2=3,14(6/2)2=3,14*9=28,26 cm2.

Odpoveď: Plocha plochej okrúhlej postavy je 28,26 cm2.

----------------------------------------- -----------

Úloha č. 2 :Nájdite S kruhu vpísaného do štvorcového obrazca a jeho polomer, ak sa jedna strana rovná a=4 viď

Riešte takto : Najprv nájdeme R=a/2=4/2=2 viď.

Teraz nájdeme obsah kruhu S=3,14*22=3,14*4=12,56 cm2.

Odpoveď: Plocha plochého kruhového útvaru je 12,56 cm2.

Plocha kruhu opísanej okolo štvorca: vzorec, príklady riešenia úloh

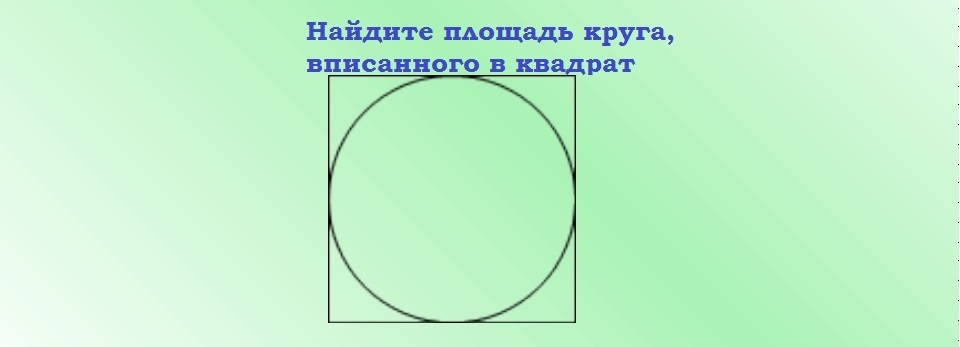
Je trochu ťažšie nájsť oblasť okrúhleho útvaru opísanú okolo štvorca. Ale ak poznáte vzorec, môžete túto hodnotu rýchlo vypočítať.

Vzorec na nájdenie S kružnice opísanej okolo štvorca:

Príklady riešenia úloh na nájdenie oblasti kruhu opísanej okolo štvorcového obrazca:

Úloha

Plocha kružnice vpísanej do pravého a rovnoramenného trojuholníka: vzorec, príklady riešenia úloh

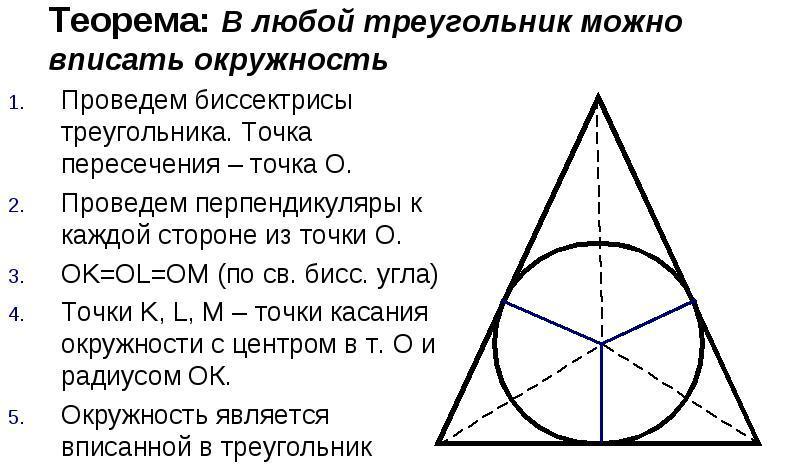
Kružnica vpísaná do trojuholníka je kružnica, ktorá sa dotýka všetkých troch strán trojuholníka. Akákoľvek trojuholníková postava môže byť napísaná kruhom, ale iba jedným. Stred kružnice bude priesečníkom priesečníkov uhla trojuholníka.

Vzorec na nájdenie plochy kruhu vpísanej do rovnoramenného trojuholníka:

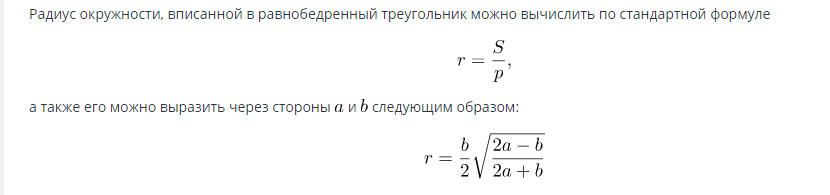
Keď je známy polomer, možno plochu vypočítať pomocou vzorca: S=πR2.

Vzorec na zistenie obsahu kružnice vpísanej do pravouhlého trojuholníka:

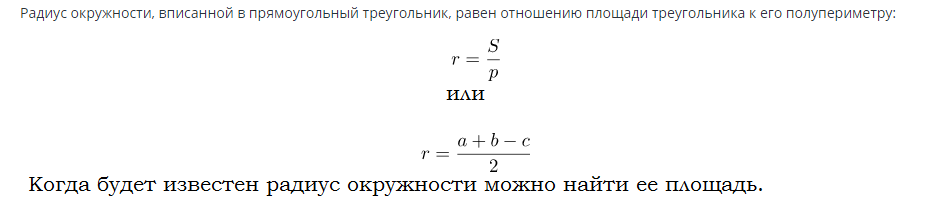
Príklady riešení úloh:

Úloha č. 1

)

Ak v tomto probléme potrebujete nájsť aj oblasť kruhu s polomerom 4 cm, môžete to urobiť podľa vzorca: S=πR2

Úloha #2

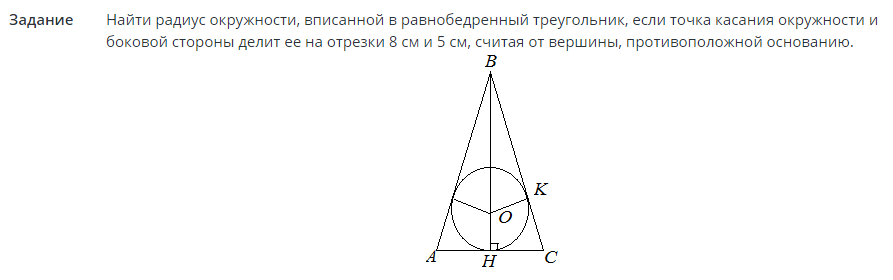
Riešenia:

Teraz, keď je známy polomer, oblasť kruhu možno nájsť z hľadiska polomeru. Pozri vzorec vyššie v texte.

Úloha #3

Oblasť kružnice opísanej okolo pravouhlého a rovnoramenného trojuholníka: vzorec, príklady riešenia úloh

Všetky vzorce pre nájdenie oblasti kruhu sa scvrkáva na skutočnosť, že najprv musíte nájsť jeho polomer. Keď je známy polomer, nájdenie oblasti je jednoduché, ako je opísané vyššie.

​​​​

Oblasť kruhu opísanej okolo pravouhlého a rovnoramenného trojuholníka sa zistí podľa nasledujúceho vzorca:

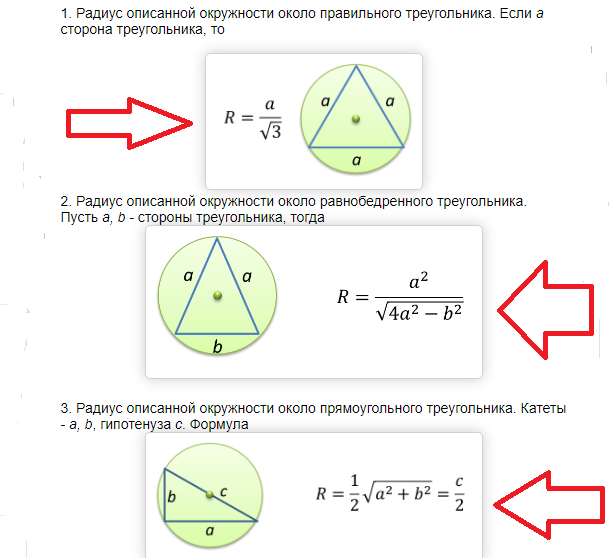
Príklady riešenia problémov:

Tu je ďalší príklad riešenia problém s použitím Heronovho vzorca.

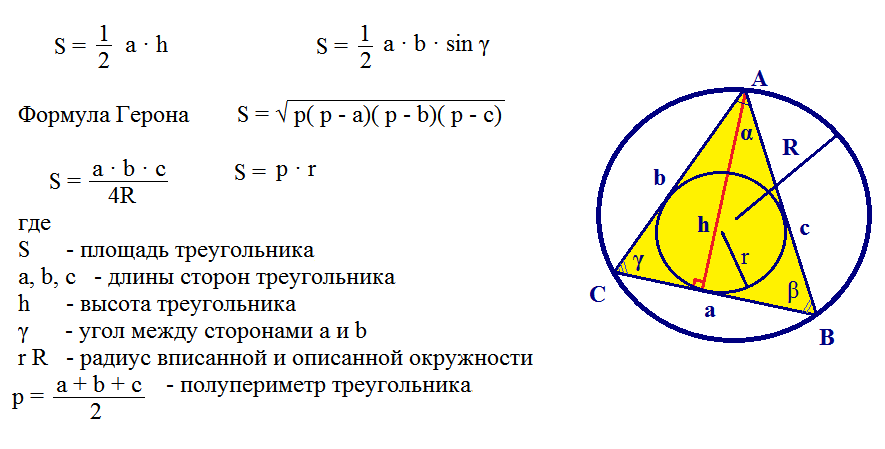
Je ťažké vyriešiť podobné problémy, ale dajú sa prekonať, ak poznáte všetky vzorce. Takéto úlohy riešia žiaci v 9. ročníku.

Plocha kruhu vpísaná do pravouhlého a rovnoramenného lichobežníka: vzorec, príklady riešenia problémov

Napríklad rovnoramenný lichobežník je vpísaný kruh, ktorý je v bode dotyku, rozdeľuje jednu stranu na segmenty m a n.

Na vyriešenie tohto problému musíte použiť nasledujúce vzorce:

Hľadanie plochy kruhu vpísaného do pravouhlého lichobežníka sa vykonáva podľa nasledujúceho vzorca:

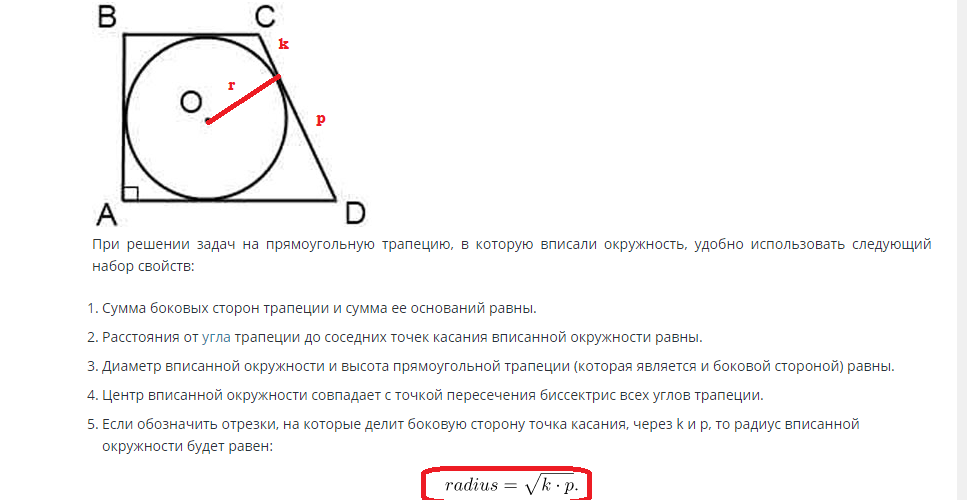
Ak je známa strana, potom polomer možno nájsť prostredníctvom tejto hodnoty. Výška strany lichobežníka sa rovná priemeru kruhu a polomer je polovica priemeru. Polomer sa teda rovná R=d/2.

Príklady riešenia úloh:

Oblasť kruhu opísanej okolo pravouhlého a rovnoramenného lichobežníka: vzorec, príklady riešenia úloh

Lichobežník možno vpísať v kruhu, keď súčet protiľahlých uhlov je 180°. Preto je možné vpísať iba rovnostranný lichobežník. Polomer na výpočet plochy kruhu opísanej v blízkosti pravouhlého alebo rovnoramenného lichobežníka sa vypočíta pomocou nasledujúcich vzorcov:

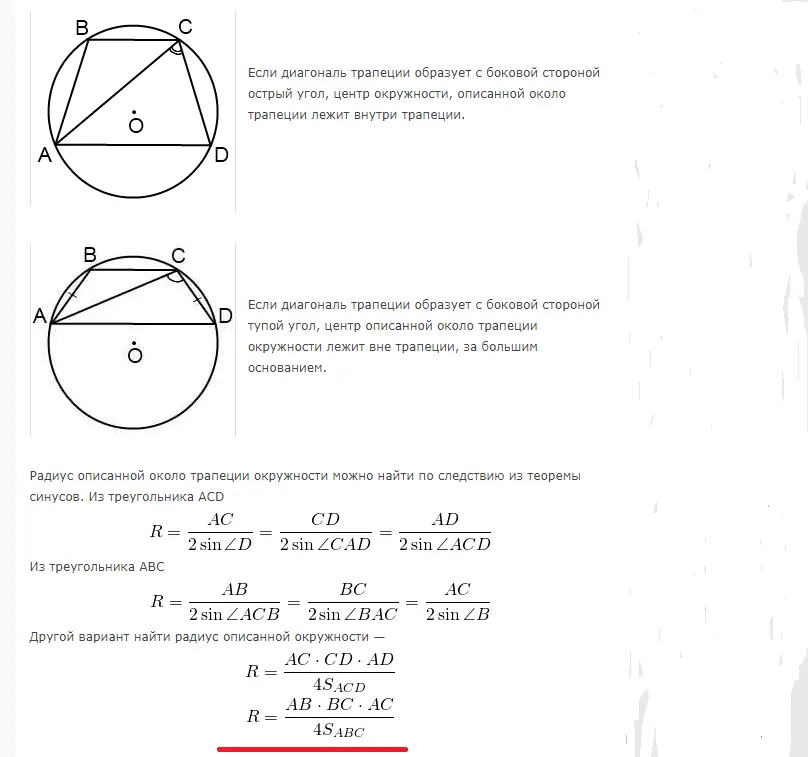
Príklady riešenia problémov:

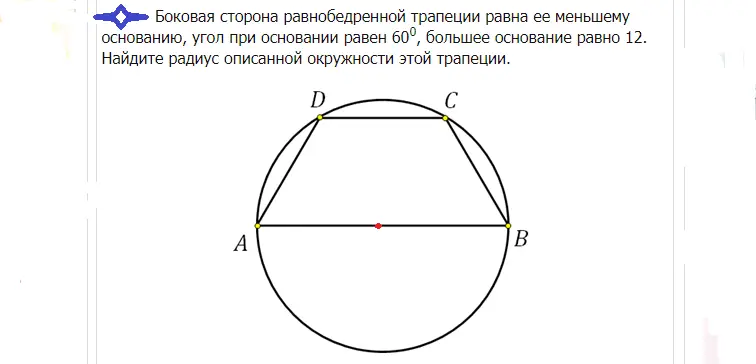
Riešenie: Veľká základňa v tomto prípade prechádza stredom, keďže do kruhu je vpísaný rovnoramenný lichobežník. Stred rozdeľuje túto základňu presne na polovicu. Ak sa základňa AB rovná 12, potom polomer R môžeme nájsť takto: R=12/2=6.

Odpoveď: Polomer je 6.

V geometrii je dôležité poznať vzorce. Nie je však možné si ich všetky zapamätať, takže aj na mnohých skúškach je dovolené použiť špeciálny formulár. Dôležité je však vedieť nájsť ten správny vzorec na riešenie toho či onoho problému. Precvičte si riešenie rôznych problémov na nájdenie polomeru a oblasti kruhu, aby ste mohli správne nahradiť vzorce a získať presné odpovede.

Video: Matematika | Výpočet plôch kružnice a jej častí